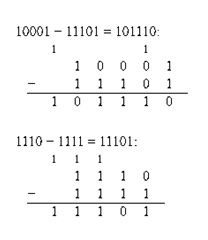Boolsk algebrakalkulator er strømmen av matematikk som består av logiske uttrykk og logiske variabler som manipulerer. Den utfører logiske operasjoner som AND, NAND, OR, NOR, NOT & X-OR . Verdiene til den boolske algebrakalkulatoren er betegnet med logikken 0 & 1. Den boolske algebrakalkulatoren bruker de grunnleggende lovene som identitetsrett, kommutativ lov, distribusjonsrett, tilknyttet lov og overtallighet. Hovedformålet med denne loven brukes til å utføre de logiske operasjonene som likhet, disjunksjon, sammenheng og implikasjon. De logiske operasjonene kan oppgis på forskjellige måter, for eksempel: konjunktjon (a ^ b) er angitt som a og b, disjunktion (a V b) er angitt som a eller b, implikasjon (a b) er angitt som en antyder b & likhet (ab) er oppgitt som p x-nor q.

Boolsk algebrakalkulator
Anvendelsen av boolsk algebra ligner på en elektrisk brytertilstand som enten kan være logiske verdier 0 og 1. Boolsk algebrakalkulator gir øyeblikkelig resultatet i form av et matematisk uttrykk ved å utføre operasjonene som tillegg, multiplikasjon osv. Den boolske kalkulator er veldig enkel og enkel å bruke. Boolean Algebra Calculator Block Diagram
Boolsk algebra kalkulatorblokkdiagram
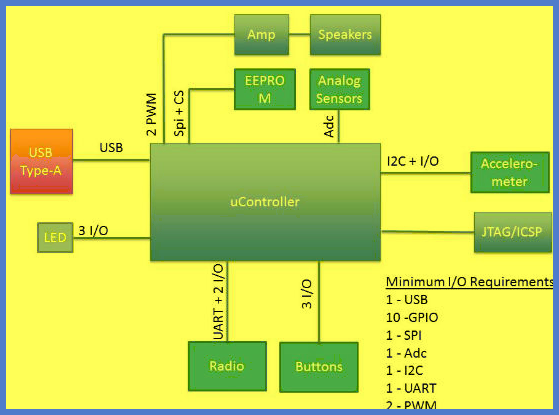
Blokkdiagrammet til boolsk algebrakalkulator inkluderer forskjellige blokker som strømforsyning , tastatur, mikrokontroller og LED display .

Boolsk algebra kalkulatorblokkdiagram
Strømforsyningen brukes til å gi strøm til uglekretsen, og den konverterer forskjellige energiformer som solenergi, mekanisk og kjemisk energi til elektrisk energi. Dette prosjektet bruker 5V energi og blir gitt til tastaturet, skjermen og mikrokontrolleren. En mikrokontroller brukes til å lese dataene fra tastaturet og sender dataene til LCD-skjerm . Mikrokontrolleren spiller en viktig rolle i dette prosjektet, og det er programmert av en Kile programvare .
I dette prosjektet brukes en trefarget LED-skjerm for å vise uttrykkets glødende mønster. Disse tofargene betyr det normale og komplement til variablene som brytere. Tastaturet i dette prosjektet brukes til å gi minimumsbetingelsene som i / p, det vil si hvert siffer på tastaturet som svarer på hver min sikt.
Boolsk algebra kalkulatorkrets
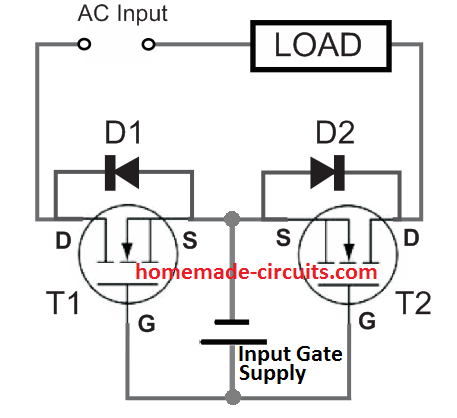
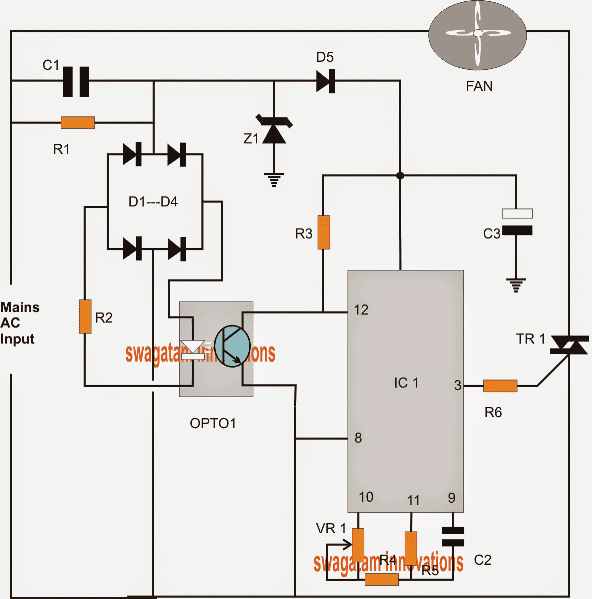
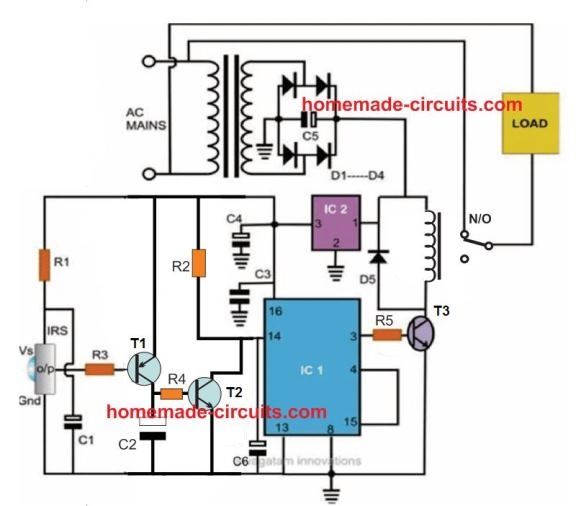
Følgende boolske kretsskjema for algebra kalkulator er billig, gir lav effekt og er pålitelig. Denne kretsen er bygget med enkel elektriske og elektroniske komponenter som er tilgjengelige i markedet som motstander, tastatur, LCD-skjerm og mikrokontroller som vist i følgende krets.

Boolsk algebra kalkulatorkrets
Ovennevnte krets består av tre variable minimizer, som bruker 'Quine MC Cluskey-algoritmen' og finner min sum av produkter ved å utføre boolske funksjoner. Denne kalkulatoren løser de boolske uttrykkene og logikkfunksjoner ved å bruke forskjellige teoremer og lover. Mikrokontrolleren som brukes i dette prosjektet spiller en viktig rolle, som er kodet med et program og styrer komponentene som brukes i denne kretsen.
Når strømforsyningen blir gitt til kretsen, blinker LED-lampen. Den blinkende LED-lampen representerer at mikrokontrolleren er klar til å motta i / ps fra tastaturet. Disse boolske uttrykkene er gitt i form av en sum av produkter (SOP).
Dette prosjektet bruker et tastatur som består av 9 brytere, hvor åtte brytere relatert til min. Vilkår som utfører produktoperasjonen og gjenværende bryter, brukes som neste knapp. Når uttrykket er angitt, slås LED av, og basert på algoritmen reduserer mikrokontrolleren minuttrykket. Deretter blinker i / p-LED-en som betyr at uttrykket minimeres og vises på LED-en.
O / p vises som en minutt på en gang, og den andre min. Vises ved å trykke på neste knapp. Så, etter å ha fått siste min. Periode, vil uttrykket reduseres og i / p-lysdioden slås AV som viser at o / p blir avsluttet. Så slås LED automatisk på for å indikere at mikrokontrolleren er klar til å ta det videre s.
Forenkling av boolsk uttrykk
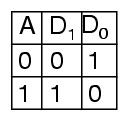
Følgende uttrykk er et eksempel på boolske uttrykk ved bruk av algebraiske teknikker.
Uttrykket er ~ (A * B) * (~ A + B) * (~ B + B) = ~ A
- ~ (A * B) * (~ A + B) * (~ B + B)
- Identitetslov og komplementlov er ~ (A * B) * (~ A + B).
- DeMorgan lov og (~ A ~ + B) * (~ A + B)
- Distribuerende lov er ~ A + ~ B * B
- ~ A er et kompliment eller en identitet.
Hvert eneste trinn gir et ligningsskjema, og reglene brukes til å løse ligningene fra de tidligere ligningene. Generelt er det forskjellige måter å nå resultatet på.
Boolske algebralover
Det er mange lover å løse de boolske uttrykkene. De boolske algebra-setningene er nemlig Idempotent Associative, Commutative, Distributive, Identity, Complement, Involution og DeMorgan’s.
Idempotent lov
A * A = A
A + A = A.
Assosiativ lov
(A * B) * C = A * (B * C)
(A + B) + C = A + (B * C)
Kommutativ lov
A * B = B * A
A + B = B + A.
Distribusjonsrett
A * (B + C) = A * B + A * C
A + (B * C) = A + B * A + C.
Identitetslov
A * 0 = 0 A *! = A
A +! =! A + 0 = A.
Komplimentlov
A * ~ A = 0
A + ~ A =!
Involusjonsloven
~ (~ A) = A
DeMorgan's lov
~ (A * B) = ~ A + ~ B
~ (A + B) = ~ A * ~ B
Hver lov i ovennevnte er beskrevet av to deler, og det er to av hverandre. Dualitetsprinsippet er å bytte ut + (OR) & * (AND) -operasjonene, 0 og 1 elementer i uttrykket.
For bedre forståelse av Boolean Algebra Calculator Circuit-konseptet, forklarte vi her en boolsk algebra-forenkling. Eksemplet på forenkling av boolsk algebra er forklart nedenfor.

Eksempel på forenkling av boolsk algebra
Ovennevnte krets er designet med to OR- og to NAND-porter, fra kretsen kan vi få ligningen som AB + BC (B + C) som er vist i figuren ovenfor. Når identitetsregelen og faktoriseringsfinalen blir brukt på kretsen ovenfor, vil det forenklede uttrykket komme i form av enkelt.
Dermed handler dette om Boolsk algebra kalkulatorkrets, boolsk algebra kalkulatorblokkdiagram, boolsk algebra kalkulatorkretsdiagram, forenkling av boolsk uttrykk, boolsk algebralov og eksempel på boolsk algebra. Vi tror at du har fått en bedre forståelse av dette konseptet, i tillegg er du i tvil angående dette emnet, vennligst gi din tilbakemelding ved å kommentere i kommentarfeltet nedenfor. Her er et spørsmål til deg, hva er bruken av boolsk algebrakalkulator?